# Import libraries
import os
import sys
import subprocess
from pathlib import Path
# Find GRASS Python packages
sys.path.append(
subprocess.check_output(
["grass", "--config", "python_path"],
text=True
).strip()
)
# Import GRASS packages
import grass.script as gs
import grass.jupyter as gj
# Create a temporary folder
import tempfile
temporary = tempfile.TemporaryDirectory()
# Create a project in the temporary directory
gs.create_project(path=temporary.name, name="xy")
# Start GRASS in this project
session = gj.init(Path(temporary.name, "xy"))
# Set region
gs.run_command("g.region", n=200, e=800, s=0, w=0, res=1)Procedural Noise

This tutorial is an introduction to generating procedural noise with Python scripting in GRASS. The computer graphics community has developed stochastic functions for procedurally modeling textures. These procedural noise functions are useful for generating synthetic data representing stochastic natural phenomena such as terrain, water, and clouds. Let’s implement procedural noise using map algebra in GRASS! This tutorial covers:
- Random walks
- Gradient noise
- Billow noise
- Ridge noise
- Fractal noise
- Multifractal noise
This tutorial can be run as a computational notebook. Learn how to work with notebooks in the tutorial Get started with GRASS & Python in Jupyter Notebooks.
Setup
Start a GRASS session in a new project with a Cartesian (XY) coordinate system. Use g.region to set the extent and resolution of the computational region. Create a region starting at the origin and extending two hundred units north and eight hundred units east.
Random Walks
In a random walk, a walker traverses a space by taking a sequence of steps in random directions. Random walks can used to simulate stochastic processes such as migration, searching, foraging, accumulation, and diffusion. Depending on the number of walkers and steps, 2-dimensional random walks can create sparse or dense stochastic surfaces, which can be useful for generating other forms of procedural noise. In GRASS, 2-dimensional random walks can be generated with the addon r.random.walk. Walkers will traverse the computational region, each stepping cell by cell in a random direction across a raster grid. The output raster records the frequency of visits per cell. First install r.random.walk with g.extension.
gs.run_command("g.extension", extension="r.random.walk")Then run r.random.walk with multiple walkers. Experiment with the parameters. Try varying the number of steps and walkers. If it runs slowly, try increasing the memory or number of processes. The resulting random walk can be used instead of an initial random or fractal surface in the following sections of this tutorial.
# Set parameters
directions = 8
steps = 50000
walkers = 10
memory = 1200
# Generate random walks
gs.run_command(
"r.random.walk",
output="walk",
directions=directions,
steps=steps,
nwalkers=walkers,
memory=memory,
flags="s",
overwrite=True
)
# Set color gradient
gs.run_command("r.colors", map="walk", color="viridis")
# Visualize
m = gj.Map(width=800)
m.d_rast(map="walk")
m.d_legend(raster="walk", color="white", at=(5, 95, 1, 3))
m.show()
Gradient Noise
The original form of gradient noise - Perlin noise - is generated by interpolating between random gradient vectors on a grid and their offsets (Perlin 1985). We will use map algebra to generate a generalized form of gradient noise by progressively smoothing a random raster surface. First create a random surface using the raster calculator r.mapcalc. Use formatted string literals to insert variables into raster calculator expressions in Python scripts. Then use a for loop to progressively smooth the random surface using nearest neighbors analysis with r.neighbors. Calculate the average neighborhood using a circular moving window. The key parameters for our gradient noise function are the seed of the pseudo-random number generator, the amplitude of the surface, the iterations of smoothing, and the wavelength of the moving window. Experiment with these parameters. Try setting different values for each of them. Then try using random walks generated with r.random.walk or a fractal surface generated with r.surf.fractal instead of a random surface.
# Set parameters
seed = 0
amplitude = 100.0
iterations = 3
wavelength = 33
# Generate random surface
gs.mapcalc(f"noise = rand({-amplitude}, {amplitude})", seed=seed)
# Generate gradient noise
for i in range(iterations):
# Smooth noise
gs.run_command(
"r.neighbors",
input="noise",
output="noise",
size=wavelength,
method="average",
flags="c",
overwrite=True
)
# Set color gradient
gs.run_command("r.colors", map="noise", color="viridis")
# Visualize
m = gj.Map(width=800)
m.d_rast(map="noise")
m.d_legend(raster="noise", at=(5, 95, 1, 3))
m.show()
Billow Noise
Billow noise or turbulence is a variation of gradient noise. After generating gradient noise, use the raster map calculator r.mapcalc to take the absolute value of the noise raster. This will transform pits and valleys into peaks and ridges and form new valleys near zero elevation, creating a billowing cloudy effect.
# Set parameters
seed = 0
amplitude = 100.0
iterations = 3
wavelength = 33
# Generate random surface
gs.mapcalc(f"noise = rand(-{amplitude}, {amplitude})", seed=seed)
# Generate perlin noise
for i in range(iterations):
# Smooth noise
gs.run_command(
"r.neighbors",
input="noise",
output="noise",
size=wavelength,
method="average",
flags="c",
overwrite=True
)
# Calculate absolute value
gs.mapcalc("turbulence = abs(noise)")
# Visualize
m = gj.Map(width=800)
m.d_rast(map="turbulence")
m.d_legend(raster="turbulence", color="white", at=(5, 95, 1, 3))
m.show()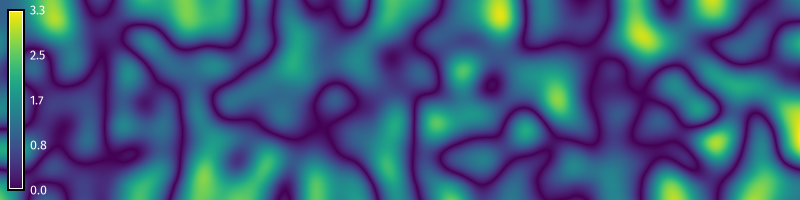
Ridge Noise
Ridge noise is another variation of gradient noise. After generating gradient noise, use the raster map calculator r.mapcalc to subtract the absolute value of the noise raster from an offset and then raise it to an exponent. This will transform the valleys of billow noise into ridges. The key parameters for our ridge noise function are the seed of the pseudo-random number generator, the amplitude of the surface, the iterations of smoothing, the wavelength of the moving window, the offset of the ridges, and the exponent for scaling the ridges.
# Set parameters
seed = 0
amplitude = 100.0
iterations = 3
wavelength = 33
offset = 10
exponent = 2
# Generate random surface
gs.mapcalc(f"noise = rand(-{amplitude}, {amplitude})", seed=seed)
# Generate perlin noise
for i in range(iterations):
# Smooth noise
gs.run_command(
"r.neighbors",
input="noise",
output="noise",
size=wavelength,
method="average",
flags="c",
overwrite=True
)
# Calculate ridge function
gs.mapcalc(f"ridge = exp({offset} - abs(noise), {exponent})")
# Visualize
m = gj.Map(width=800)
m.d_rast(map="ridge")
m.d_legend(raster="ridge", at=(5, 95, 1, 3))
m.show()
Fractal Noise
Fractional Brownian motion is a random walk through space that is contingent on past steps and has self-similar fractal properties. Fractal noise can be generated from fractional Brownian motion by accumulating octaves, i.e. iterations, of procedural noise with incremental changes in frequency and amplitude (Musgrave 2003, Vivo & Lowe 2015, Quilez 2019). First, use the raster map calculator r.mapcalc to create a constant surface. Then use a for loop to iterate through each octave. For each octave, generate gradient noise, add the gradient noise to the prior surface using r.mapcalc, and then increment the function’s fractal parameters. The key parameters for our fractal Brownian motion function are the seed of the pseudo-random number generator, the amplitude of the surface, the iterations of smoothing, the wavelength of the moving window, the octaves for accumulating noise, the lacunarity or change in frequency of each octave, and the gain in amplitude for each octave.
# import libraries
import random
# Set parameters
seed = 0
amplitude = 100.0
iterations = 3
wavelength = 33
octaves = 6
lacunarity = 0.5
gain = 0.2
# Generate zeros
gs.mapcalc("fbm = 0")
# Generate fractional Brownian motion
for octave in range(octaves):
# Generate random surface
gs.mapcalc(f"noise = rand(-{amplitude}, {amplitude})", seed=seed)
# Generate gradient noise
for i in range(iterations):
# Smooth noise
gs.run_command(
"r.neighbors",
input="noise",
output="noise",
size=wavelength,
method="average",
flags="c",
overwrite=True
)
# Calculate sum of gradient noise maps
gs.mapcalc("fbm = fbm + noise")
# Increment parameters
amplitude = amplitude * gain
wavelength = round(wavelength * lacunarity)
if wavelength % 2 == 0:
wavelength += 1
# Visualize
m = gj.Map(width=800)
m.d_rast(map="fbm")
m.d_legend(raster="fbm", at=(5, 95, 1, 3))
m.show()
Multifractal noise
Multifractal noise can be generated by more complex incremental accumulations of procedural noise (Musgrave et al. 1989, Musgrave 2004). In this example we will model multifractal Brownian motion by accumulating octaves of turbulent fractal gradient noise. First, use the raster map calculator r.mapcalc to create a constant surface. Then use a for loop to iterate through each octave. For each octave, generate a fractal surface with r.surf.fractal, progressive smooth this surface in a nested for loop to model fractal gradient noise, add the absolute value of fractal gradient noise to the prior surface scaled by amplitude, and then increment the function’s fractal parameters. Experiment with different parameters. Try multiplying fractal maps instead of adding them, but be sure to start with a non-zero constant to avoid multiplication by zero. The key parameters for our multifractal function are the seed of the pseudo-random number generator, the dimension of the fractal surface, the amplitude of the multifractal surface, the iterations of smoothing, the wavelength of the moving window, the octaves for accumulating noise, the lacunarity of each octave, and the gain in amplitude for each octave.
# Set parameters
seed = 0
amplitude = 0.1
iterations = 3
wavelength = 33
octaves = 6
lacunarity = 0.5
gain = 0.05
dimension = 2.2
# Generate zeros
gs.mapcalc("multifractal = 0")
# Generate multifractal surface
for octave in range(octaves):
# Generate fractal surface
gs.run_command(
"r.surf.fractal",
output="fractal",
dimension=dimension,
seed=seed
)
# Generate fractal gradient noise
for i in range(iterations):
# Smooth noise
gs.run_command(
"r.neighbors",
input="fractal",
output="fractal",
size=wavelength,
method="average",
flags="c",
overwrite=True
)
# Calculate sum of fractal maps
gs.mapcalc(f"multifractal = multifractal * {amplitude} + abs(fractal)")
# Increment parameters
dimension = dimension + gain
amplitude = amplitude + gain
wavelength = round(wavelength * lacunarity)
if wavelength % 2 == 0:
wavelength += 1
# Visualize
m = gj.Map(width=800)
m.d_rast(map="multifractal")
m.d_legend(raster="multifractal", color="white", at=(5, 95, 1, 3))
m.show()
References
Gonzalez Vivo, Patricio, and Jen Lowe. 2015. “Fractal Brownian Motion.” In The Book of Shaders. https://thebookofshaders.com/13/.
Mandelbrot, Benoît B. 1983. The Fractal Geometry of Nature. W.H. Freeman.
Musgrave, Forest K., Craig E. Kolb, and Robert S. Mace. 1989. “The Synthesis and Rendering of Eroded Fractal Terrains.” ACM SIGGRAPH Computer Graphics (New York, NY, USA) 23 (3): 41–50. https://doi.org/10.1145/74334.74337.
Musgrave, Forest Kenton. 2003. “Procedural Fractal Terrains.” In Texturing and Modeling, Third Edition, edited by David S. Ebert, Forest Kenton Musgrave, Darwyn Peachey, et al. The Morgan Kaufmann Series in Computer Graphics. Morgan Kaufmann. https://doi.org/10.1016/B978-155860848-1/50045-0.
Musgrave, Forest Kenton. 2004. “Fractal Terrains and Fractal Planets.” In The Elements of Nature: Interactive and Realistic Techniques, edited by Oliver Deusen, David S. Ebert, Ron Fedkiw, et al. SIGGRAPH ’04. Association for Computing Machinery. https://doi.org/10.1145/1103900.1103932.
Perlin, Ken. 1985. “An Image Synthesizer.” ACM SIGGRAPH Computer Graphics (New York, NY, USA) 19 (3): 287–96. https://doi.org/10.1145/325165.325247.
Quilez, Inigo. 2019. “Fractional Brownian Motion.” https://iquilezles.org/articles/fbm/.